Generelle Transformationstechnik
Bei einer Koordinatentransformation werden Koordinaten von einem Koordinatensystem in ein anderes übertragen. Formal gesehen ist dies der Übergang von den ursprünglichen Koordinaten (x1,x2,...,xN) zu den neuen Koordinaten (x'1,x'2,...,x'N).
Typische Transformationsvorgänge sind: Translation (Verschiebung), Rotation (Drehung) und Veränderung des Maßstabs (Skalierung).
|
|
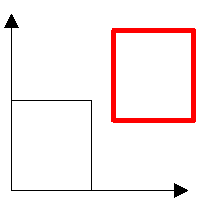
Translation (Verschiebung) Eine Translation kann als Verschiebung des Koordinaten-ursprungs gedeutet werden. Im 2D-Raum erfordert eine Translation zwei Parameter: Verschiebung in x-Richtung (tx) und in y-Richtung (ty). |
|
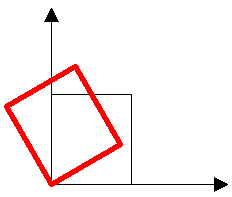
Rotation (Drehung) Bei einer Rotation wird das Koordinatensystem gedreht. Auch dieser Vorgang ist als Drehung der abgebildeten Objekte einfacher vorstellbar. In zwei Dimensionen gibt es nur einen Rotationswinkel als Parameter. |
|
|
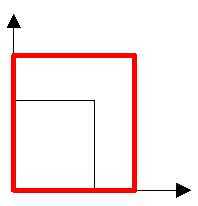
Skalierung Bei der Skalierung werden die „Einheiten“ der Achsen geändert. Ein Spezialfall ist die „Maßstabs-Änderung“, bei der alle Faktoren den gleichen Wert haben. |
|
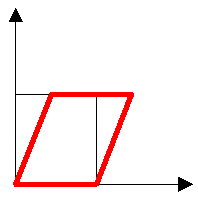
Scherung Bei der Scherung verändert sich der Winkel zwischen den Koordinatenachsen. Im 2D-Raum gibt es daher nur einen Parameter. |
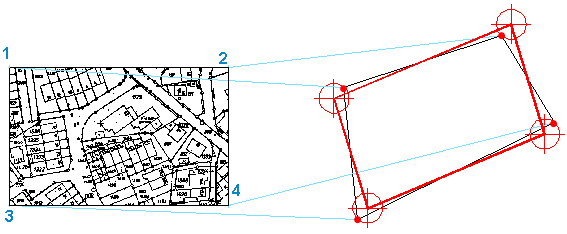
Affine Transformationen bestehen aus einer oder mehreren dieser einfachen Transformationen. Die beteiligten Koordinatensysteme sind hierbei linear, d. h. im Prinzip durch einen Koordinatenursprung und gleichmäßig unterteilte Koordinatenachsen gegeben. Mit Hilfe der hier zur Anwendung kommenden Polynom-Methode wird das gesamte Bild transformiert, sodass es so genau wie möglich mit den angegebenen Kontrollpunkten übereinstimmt.
|
|
In Abhängigkeit des Pixelbilds oder der PDF-Unterlage entsprechen die tatsächlichen Zielpunkte nicht immer den ausgewählten Zielpunkten. Der daraus resultierende Fehler wird als numerischer Wert im Dialog angegeben, nachdem die Kontrollpunkte eingegeben wurden. |
Der Fehler wird für jeden Punkt als Abstand zwischen dem vorgesehenen und dem tatsächlichen Punkt gemessen und mit der nachfolgenden Formel berechnet.
![]()
Der gesamte RMS-Fehler (Root Mean Square) des Bildes wird mit Hilfe der folgenden Formel berechnet:
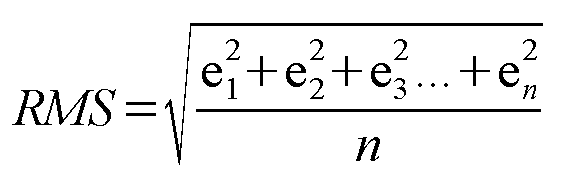
|
Anmerkung: PDF-Unterlagen sind PDF-Dateien, die wie Rasterbilder als Ganzes extern referenziert sind. Bei der Transformation wird keine Verzerrung unterstützt. PDF-Unterlagen können daher nur skaliert und gedreht werden. |