Abrechnung

Die Abszisse, zusammen mit den Loten der Messpunkte (Ordinaten) auf die Abszisse, zerlegt die Fläche in Allgemeine Trapeze, bei denen es sich anschaulich gesehen um folgende Typen von Figuren handeln kann:

• Normales Trapez – mit Basisseite a (Ordinatenwert des aktuellen Messpunktes auf die Abszisse), Parallele Seite b (Ordinatenwert des nächsten Messpunktes auf die Abszisse) und Höhe h (Zuwachs des Abszissenwertes vom aktuellen zum nächsten Messpunkt). Damit so ein normales Trapez entsteht, müssen die beiden Ordinatenwerte das gleiche Vorzeichen haben.

• Dreieck – ist ein Sonderfall von a), in dem einer der Ordinatenwerte Null ist.

• Verschränktes Trapez – ist ein Sonderfall von a), in dem die beiden Ordinatenwerte verschiedene Vorzeichen haben (beide ungleich Null).

• Degeneriertes Trapez – ist ein Sonderfall von a), in dem beide Ordinatenwerte Null sind oder der Abszissenzuwachs Null ist. Dieser Fall liefert keinen Beitrag zur Fläche und wird daher ausgespart.

Damit ist die Berechnung der Fläche auf die Berechnung der Flächen der drei einfachen Grundfiguren a), b) und c) zurückgeführt. Allerdings können gemäß der obigen Beschreibung der Figurtypen a), b) und c) negative Werte bei den Seiten und Höhen der Figuren auftreten. 

Erfreulicherweise erhält man aber stets die richtige Fläche, wenn man die Formel zur Berechnung der Trapezfläche A(1) A = (a+b)h/2 verwendet und dabei auch negative Werte von a, b und h zulässt.

Sieht man zunächst von möglichen negativen Vorzeichen ab, so ist leicht einzusehen, dass der Figur-Typ b) mit a=0 bzw. b=0 die Formel zur Berechnung einer Dreiecksfläche ergibt: A = ah/2   bzw.   A = bh/2

Im Fall c) eines verschränkten Trapezes ist nicht unmittelbar ersichtlich, dass die Trapezflächenformel (1) den richtigen Beitrag liefert. Dies wird daher im Folgenden erläutert:

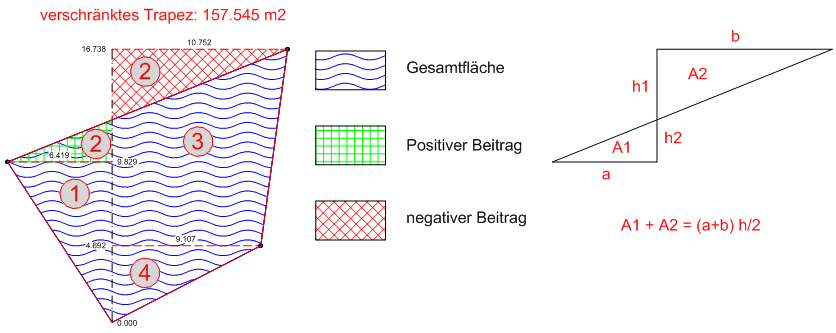
Ein verschränktes Trapez besteht aus zwei Dreiecken mit:

1. Dreieck: Grundseite a (der Wert der aktuellen Ordinate ohne Vorzeichen), Höhe h1 und Fläche A1

2. Dreieck: Grundseite b (der Wert der nächsten Ordinate ohne Vorzeichen), Höhe h2 und Fläche A2

wobei für die Höhe h des verschränkten Trapezes gilt: (2)  h=h1+h2

Man kann nachrechnen, dass die Summe dieser beiden Dreiecksflächen auch sofort mit der Trapezformel (1) berechnet werden kann, wenn man dort einen negativen Wert für die erste oder die zweite Ordinate zulässt. 

Im Folgenden wird der Fall behandelt, in dem die zum 1. Dreieck gehörige Ordinate positiv und die zum 2. Dreieck gehörige Ordinate negativ ist. (Der andere mögliche Fall, erste Ordinate negativ und zweite Ordinate positiv, liefert bei der entsprechenden Rechnung das entsprechende Ergebnis.)

Eine Umformung der Formel (3)  A1 + A2 = ah1/2 + bh2/2 ergibt (4)  A1 + A2 = ((a-b)h1 + bh)/2

Aus dem Strahlensatz folgt:  a/b = h2/h1 also wegen der Beziehung (2)  a/b = (h-h1)/h1

Daraus kann man h1 berechnen:  h1 = ah/(a+b)

Dies in (4) eingesetzt ergibt nach einer Vereinfachung der rechten Seite die Gleichung (5)

A1 + A2 = (a-b)h/2

Vergleicht man nun (5) mit der Trapezflächenformel (1), sieht man, dass ein negativer Wert von b in Formel (1) gerade die Summe der beiden Dreiecksflächen liefert.

Denn, ersetzt man in Formel (3) b durch -b, so wird (5) zu (6)  A1 + A2 = (a+b)h/2

Schaut man jetzt nochmal auf die Beziehung (3), so sieht man, dass das 2. Dreieck einen negativen Flächenbeitrag liefert. 

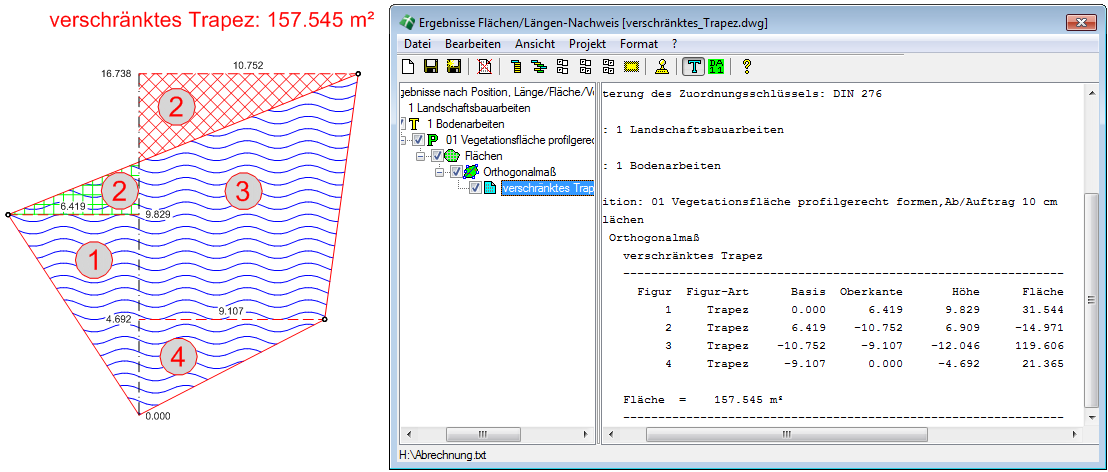
In dem dargestellten Beispiel korrigiert dieser negative Flächenbeitrag A2 (hier 2 rechts) die Fläche des nachfolgenden Trapezes (hier 3). Man beachte, dass z. B. das nachfolgende Trapez die beiden negativen Ordinaten a und b sowie einen negativen Abszissenzuwachs h hat, so dass (1) die richtige positive Fläche liefert.